In this post we’re going to have a look at the basics of statistical relationships – correlation analysis and statistical associations – learn what they are and how you use them (without being burdened by statistical detail – I’ll deal with the details in other posts).
I’ll also introduce the basics of how to use association and correlation analysis to build a holistic strategy to discover the story of your data using univariate and multivariate statistics - and we’ll also find out why eating ice cream does not make you more likely to drown when you go swimming.
You’ll learn about the null hypothesis and why it’s so important to statistics, p-values and a sensibly chosen cut-off value, and learn about how to measure the strength of relationships with Odds Ratios.
I blame Florence Nightingale. Really, I do.
She publishes one little pie chart and suddenly we’re all expected to be statisticians.
Gone are the days when a scientist can collect their data, then simply hand it over to a statistician for analysis and return in 6 months for the results. Oh no, now we all have to do our own analyses – with little or no training!
Cheers Flo…
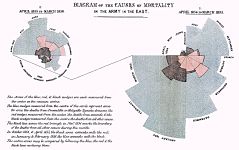
Diagram of the Causes of Mortality by Florence Nightingale, illustrating how most of the fatalities from the Crimean War were from sickness rather than wounds
So what can you do about it? Well, learning how to do effective and efficient data analysis would be a good start…
…and we’re here to help!
In previous blog posts I’ve talked about data collection techniques, data cleaning and tips for data classification.
If you’ve done a good job then you now have a dataset that is fit for purpose and is ready for analysis.
Ready to learn more about correlation analysis?
If you're in a hurry and want something that will give you a holistic strategy to analyse your statistical correlations, check out my book Associations and Correlations.
Disclosure: This post contains affiliate links. This means that if you click one of the links and make a purchase we may receive a small commission at no extra cost to you. As an Amazon Associate we may earn an affiliate commission for purchases you make when using the links in this page.
You can find further details in our TCs
What are Statistical Associations and Correlation Analysis?
Did you know that statistics can never prove that there is (or is not) a relationship between a pair of variables?
If that’s the case, then what is the point of statistics, I hear you ask…
Well, statistics is the study of uncertainty. If you’ve already proven beyond all doubt that a relationship exists between this and that, then there is nothing to be gained from a statistical analysis. It is only when there is uncertainty about the relationship that we can learn something from a statistical analysis. It is for this reason that statistics can neither prove nor disprove the existence of a relationship. It can only tell you how likely or unlikely that a relationship is.
But what is a statistical relationship?
When you can phrase your hypothesis (question or hunch) in the form of:
- Is smoking related to lung cancer?
- Is there an association between diabetes and heart disease?
- Are height and weight correlated?
then you are talking about the relationship family of statistical analyses, which include statistical associations and correlation analysis.
Typically, the terms correlation, association and relationship are used interchangeably by researchers to mean the same thing. That’s absolutely fine, but when you talk to a statistician you need to listen carefully – when she tells you to do a correlation analysis, she is most probably talking about a statistical correlation test, such as a Pearson correlation.
There are distinct stats tests for correlations and for associations, but ultimately they are all testing for the likelihood of relationships in your data.
When you are looking for a relationship between 2 continuous variables, such as height and weight, then the test you use is called a correlation. If one or both of the variables are categorical, such as smoking status (never, rarely, sometimes, often or very often) or lung cancer status (yes or no), then the test is called an association.
Correlation Analysis
If there is a correlation between one variable and another, what that means is that if one of your variables changes, the other is likely to change too.
For example, say you wanted to find out if there was a relationship between age and percentage of body fat. You would do a scatter plot of age against body fat percentage, and see if the line of best fit, aka a regression line, is horizontal. If it is not, then we can say there is a correlation, like this:
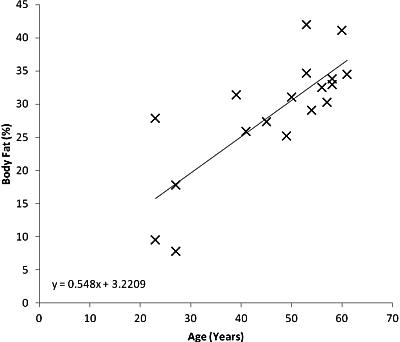
Scatter plot illustrating a positive correlation between Age and Percentage of Body Fat
In this example, there is a positive correlation between age and percentage of body fat; that is, as you get older you are likely to gain increasing amounts of body fat. Ah, the joys of getting old…
You can test whether the correlation is statistically significant by using an appropriate test, such as a Pearson correlation test or Spearman correlation test (more on these in a future blog post).
Take a look at the scatter plot above. Do you think that the result of the correlation analysis is likely to be statistically significant?
Looking at the best fit line, what would be your expected increase in body fat percentage over the next decade? [Clue: rather than guess from the regression line you could calculate it from the gradient shown in the equation of the line].
Related Books
Statistical Associations
For associations it is all about the measurement or counts of variables within categories.
Let’s have a look at an example from Charles Darwin. In 1876, he studied the growth of corn seedlings. In one group, he had 15 seedlings that were cross-pollinated, and in the other he had 15 that were self-pollinated. After a fixed period of time, he recorded the final heights of each of the plants.
To analyse these data you pool together the heights of all those plants that were cross-pollinated, work out the average height and compare this with the average height of those that were self-pollinated. You can display the results as a Histogram, like this:
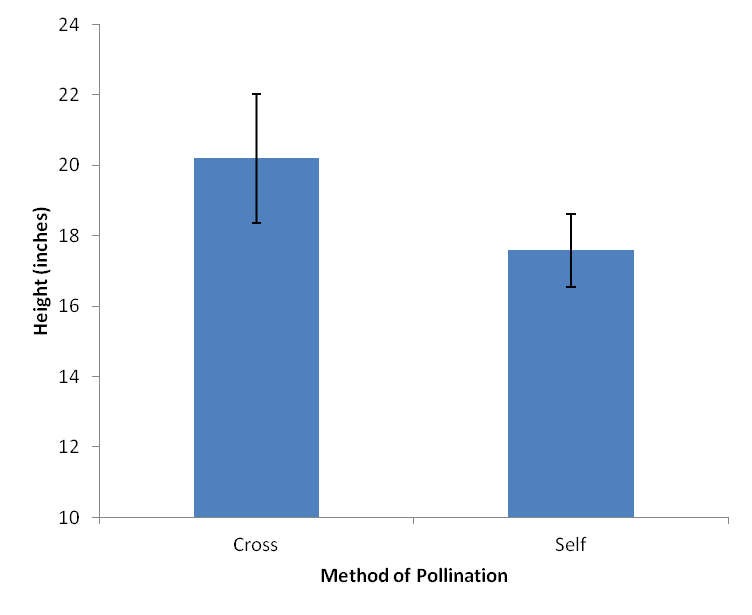
Histogram showing the average height of Darwin’s cross-pollinated and self-pollinated seedlings. Variation is shown by 95% confidence intervals.
Of course, Darwin found that not all cross-pollinated and self-pollinated plants were exactly 20.19 and 17.59 inches tall, there was a certain amount of variation in their heights. This variation can be expressed by the standard deviation, variance or other appropriate measure, like the 95% confidence intervals shown.
A statistical test (most likely a 2-sample t-test or Mann-Whitney U-test – more on those in a future post) can tell you whether there is a significant difference between the heights of the cross-pollinated and self-pollinated plants.
What I like about using 95% confidence intervals rather than standard deviations is that 95% confidence intervals are related to the statistical tests that you use to decide whether there is likely to be a statistically significant difference between the measurements, so you can usually assess by eye whether there might be a difference.
For Darwin’s corn seedlings, if there is a clear separation between the confidence intervals (in other words, little or no cross over between them) then there is likely to be a statistically significant difference between the heights of the cross-pollinated and self-pollinated plants.
Looking at the histogram and 95% confidence intervals above, do you suspect there is a significant difference between the heights of the cross- and self-pollinated plants?
What do you think the histogram and confidence intervals would look like if Darwin had performed this experiment with just 5 plants in each group rather than 15? Would there have been a significant difference between the seedling heights?
What do you think would happen to the confidence intervals if Darwin had repeated this experiment with 30 plants in each group?
Using Association and Correlation Analysis to Discover the Story of Your Data
OK, so let’s say you have your hypothesis, you’ve designed and run your experiment, and you’ve collected your data. So how do you use association and correlation analysis to discover the story of your dataset?
If you’re a medic, an engineer, a businesswoman or a marketer then here’s where you start to get into difficulty. Most people who have to analyse data have little or no training in data analysis or statistics, and round about now is where the panic starts to begin.
What you need to do is:
- Take a deep breath
- Define a strategy of how to get from data to story
- Learn the basic tools of how to implement that strategy (learning about associations and correlations is a good first step)
In relationship analysis, the strategy is a fairly straightforward one and goes like this:
- Clean & classify your data
- You now have a clean dataset ready to analyse
- Answer your primary hypothesis
- This is related to that
- Find out what else has an effect on the primary hypothesis
- Rarely is this related to that without something else having an influence
Not too difficult so far is it?
OK, now the slightly harder bit – you need to learn the tools to implement the strategy. This means understanding the statistical tests that you’ll use in answering your hypothesis.
There are basically 2 types of test you’ll use to investigate associations and correlations:
- Univariate statistics
- Multivariate statistics
They sound quite imposing, but in a nutshell, univariate stats are tests that you use when you are comparing variables one at a time with your hypothesis variable. In other words, you compare this with that whilst ignoring all other potential influences.
On the other hand, you use multivariate stats when you want to measure the relative influence of many variables on your hypothesis variable, such as when you simultaneously compare this, that and the other against your target.
It is important that you use both of these types of test because although univariate stats are easier to use and they give you a good feel for your data, they don’t take into account the influence of other variables so you only get a partial – and probably misleading – picture of the story of your data.
On the other hand, multivariate stats do take into account the relative influence of other variables, but these tests are much harder to implement and understand and you don’t get a good feel for your data.
I’ll discuss the finer details of each of these analysis modalities in future blog posts, but for now, my advice is to do univariate analyses on your data first to get a good understanding of the underlying patterns of your data, then confirm or deny these patterns with the more powerful multivariate analyses. This way you get the best of both worlds and when you discover a new relationship, you can have confidence in it because it has been discovered and confirmed by two different statistical analyses.
When pressed for time I’ve often just jumped straight into the multivariate analysis. Whenever I’ve done this it always ends up costing me more time – I find that some of the results don’t make sense and I have to go back to the beginning and do the univariate analyses before repeating the multivariate analyses.
I advise that you think like the tortoise rather than the hare – slow and methodical wins the race…

CorrelViz - All The Correlations in Your Data In Minutes, Not Months
Discover new insights - Save time and money
Association & Correlation Analysis - Summary
Well, I hope you got something useful out of this blog post.
We’ve discovered that association and correlation analyses are really just statistical tests to find out if relationships exist between variables, that statistical significance can often be judged by eye if an appropriate visualisation is used, and that having a holistic strategy to discovering all the relationships in your dataset will make your analysis go that bit smoother.
Oh, yes – we’ve also discovered that the Lady With The Lamp did us all a huge favour. By learning about data, analysis and statistics we’ve discovered that we can understand our investigations and the processes much more, giving us a much deeper understanding of science, nature, medicine and the world around us.
Thanks Aunt Flo.

DID YOU FIND IT USEFUL?
Pin it to your favourite board so it's always handy!

